Many ways to increase current transformer

How to increase the transformer currents? If your load is not a full running. The most cause comes from a lower current of the transformer. But changing them is difficult and expensive.

It is a pity if you need to buy a new transformer. So, let’s look at how to modify it to increase the current up.

These ways may help you!

Since the most transformers always are the center tap form for a dual power supply.  Such as  the transformer in Figure

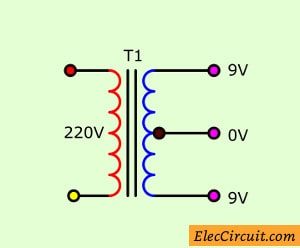
The 230V/110V AC primary to 9V-0-9V,1A secondary transformer.  It includes 9V,1A x 2 secondary coil that connects in series.

In normal, we can easily apply it as 18V,1A output without using the CT terminal.

Also, we can use it as 9V 2A by how to take both coils to connects in parallel.

See Figure 2. But it must be connected to a matching phase of a signal. (It’s like connecting batteries in parallel)

Thus, we must separate both the wires apart. Then, connect them as Figure just only. We will have the 9V,2A transformer by without the center tap terminal.

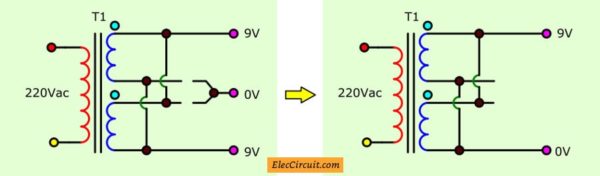
REMEMBER: Do not connect the coils wrong polarity. Because they are like a short circuit!

See: Simple Electronics Circuits

Why short circuit
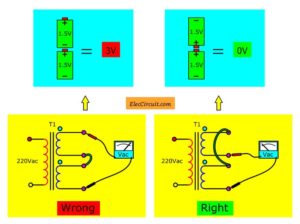
The battery has polarity.  Also, the coil of the transformer has polarity or direction of current flowing.  Look at below!

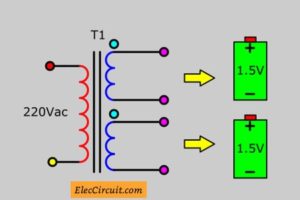
Imagine two 1.5V batteries are connected together in parallel for double the current.
Look at the Figure below.

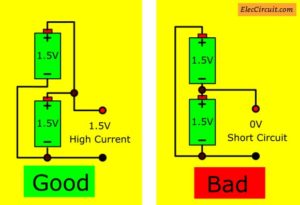
If a bad connecting, it is wrong. The voltage is zero and short circuit (Right). The batteries can be damaged.

We need a good connecting. It will still output is 1.5V but high current about 2 times.

Check the correct transformer connecting

If we are afraid of a wrong connection.  It is easy to check.  As Figure below. First, connect a wire to 2 terminals. Then, measure AC voltage at another 2 terminal. If it is high voltage, it is wrong (left).

Next, turn the wire to another 2 terminal. Then check it again.  It should be zero volts. It is a correct connecting.

Are you clear?

But in practice really we will see that the output current isn’t 2 times. So use next ways.

Increase current using Rectifier

This way have a difference as detail below.

Suppose, we use 1A transformer in general circuit will be the full wave rectifier that has the center trap as Figure.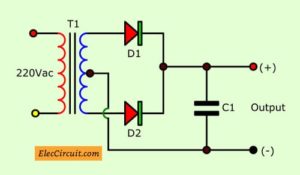

Full wave rectifier using center tap transformer

This makes the output current is reduced to 0.8A. Which it is not full of 1A.

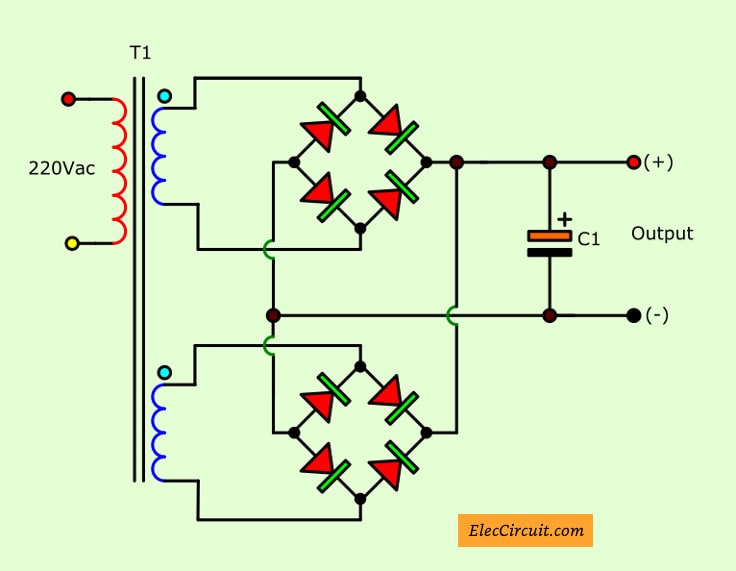
Then we take the complete 2A transformer above, apply in the circuit as Figure 4 by the bridge full wave rectifier.

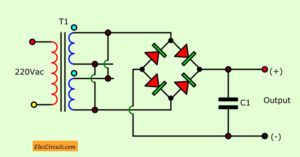
But we see that the maximum current higher than 1.3 times only.

In practice may be a problem. Because of phase and voltage is not the same.

See: More Power supply circuits

Which we can improve by separating each rectifier diodes out. Then, connect them in parallel together. As Figure below.

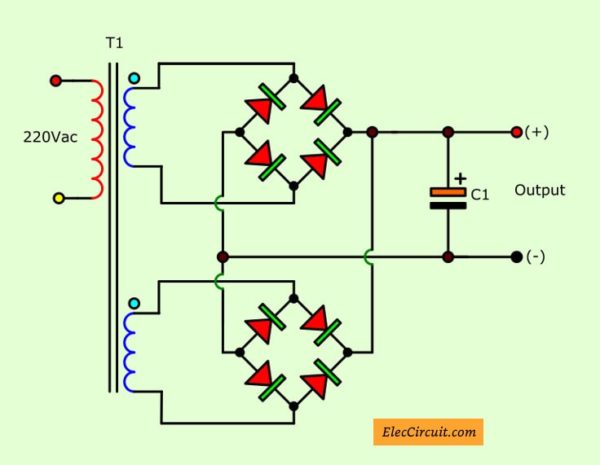
Keep reading: Boosting Regulator Current

Related Posts

Apichet Garaipoom

I love electronics. I have been learning about them through creating simple electronic circuits or small projects. And now I am also having my children do the same. Nevertheless, I hope you found the experiences we shared on this site useful and fulfilling.